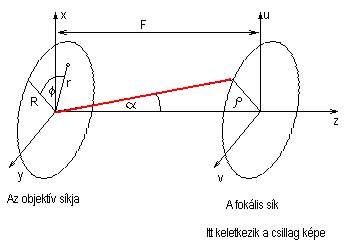
2.Fényelhajlás (diffrakció) kör alakú nyíláson (Lencsés távcsövekben)
|
Itt az probléma hengeres szimetriát mutat, így tehát illene az r,f, z
hengerkoordinátákat bevezetni.
Az útkülönbség:
r cos f sin a
A fáziskülönbség :
![[Maple Plot]](images/res10.gif)
Itt egy felületi integrált kell kiszámítani, mégbedig az xOy síkbeli R sugarú körlemezen lévő dS felületelemeken másodlagos hullámforrásokat helyezünk el, a Huyghens-Fresnel elvnek megfelelően.
Az innen kiinduló hullámokat összegezzük az alábbi kettős integrállal:
![[Maple Plot]](images/res11.gif)
|
Nos ezt hengerkoordinátákban integráljuk, a dS területelemet az alábbi ábra szerint az r df dr-ként számoljuk ki:
![[Maple Plot]](tav2.gif)
Ezáltal a fenti területintegrál így néz ki:
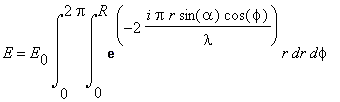
Ez egy macerás integrál, nem egy mai főiskolásnak való... Szerencsére azonban az ilyen típusú integrálokat a speciális matematika ismeri. Először a f változó szerint integrálunk, majd az r szerint. A f szerinti integrál a következő típusú:
![[Maple Plot]](images/specmat1.gif)
ahol
![[Maple Plot]](images/specmat2.gif)
Másfelől az elsőfajú Bessel függvények generátorfüggvénye:
![[Maple Plot]](images/specmat3.gif)
ahol Jn(x)az n-edrendű elsőfajú Bessel függvény.
Ebben végezzük el az x=q és
![[Maple Plot]](images/specmat4.gif)
változócseréket, majd vegyük figyelembe a
![[Maple Plot]](images/specmat5.gif)
azonosságot. Ekkor a következő képletet kapjuk:
![[Maple Plot]](images/specmat6.gif)
Ezt integráljuk 0 és 2p között:
![[Maple Plot]](images/specmat7.gif)
No azt már könnyű belátni, hogy a jobboldal második integrálja nulla.
Marad tehát a jobboldali első integrál, ami viszont nem függ f-től, így értéke 2p J0(q).
Visszatérve az elektromos mező integráljához:
![[Maple Plot]](images/res15.gif)
Most az r szerint integrálunk, egészen a távcsőnyílás pereméig, vagyis R-ig. Ez az integrál már könnyebb:
![[Maple Plot]](images/res16.gif)
Itt a J1(x) az elsőfajú elsőrendű Bessel függvény.
Hogyan változik a térerősség a fokális sík r iránya mentén?
Ennek meghatározásához figyelembe vesszük azt, hogy az a szög nagyon kicsi, így a sin a hozzávetőleg egyenlő a tg a-val, így
![[Maple Plot]](images/res17.gif)
Most pedig vezessűk be a következő jelölést:
![[Maple Plot]](images/res18.gif)
Ezzel a térerősséga következő alakban írható:
![[Maple Plot]](images/res19.gif)
A fény intenzitáseloszlását a az E*Ekonjugált adja:
![[Maple Plot]](images/res20.gif)
Egy ilyen függvényt ábrázol az alábbi grafikon:
![[Maple Plot]](images/res21.gif)
A függvény maximumát itt egységnyire vettük.
Ezt a függőleges tengely körül megforgatva kapjuk a síkbeli fényintenzitás eloszlását:
![[Maple Plot]](images/res22.jpg)
Ezt természetesen egy ernyőre felfogatva valami ilyesmit látunk:
![[Maple Plot]](images/res23.gif)
Nos, ilyennek látszik egy csillag képe egy lencsés távcsőben, ideális esetben, erősen felnagyítva.
A középső pacni az úgynevezett Airy-korong, a körülötte halványan sejlő
gyűrű az első diffrakciós gyyűrű. A második gyűrű már nagyon halvány.
Namost az Airy-korong mérete egy jó kukkerban
ezredmilliméter nagyságrendű.
3.A fénymennyiség eloszlásának számítása lencsés távcsövekben
A kiinduláshoz használt képlet:
![[Maple Plot]](images/res20.gif)
Az Airy korongba eső fényhányadot úgy kapjuk meg, hogy kiszámítjuk a fenti
felület és a vízszintes sík által közrezárt térfogatot (V), majd az
Airy-korong alatti térfogatot (V1), majd ebből képezzük a V1/V arányt.
Lássuk tehát V-t:
![[Maple Plot]](images/refreloszl4.gif)
A f szerint integrálva:
![[Maple Plot]](images/refreloszl5.gif)
Ennek értéke:
![[Maple Plot]](images/refreloszl6.gif)
Az egyszerűség kedvéért legyen R=1 és q=1. Ekkor
V=39.47841762
Az Airy korongba jutó fénymennyiséget úgy számítjuk ki, hogy a J1(x)=0
egyenlet első megoldásáig (az Airy korong széléig) integrálunk. Jelöljük ezt az értéket
l1-gyel. Ezzel
![[Maple Plot]](images/refreloszl7.gif)
Az integrálás után ezt kapjuk:
![[Maple Plot]](images/refreloszl8.gif)
Ennek értéke R=1 és q=1-re, továbbá l1=3.831705970...
V1=33.07442094
Az Airy-korongba jutó hányadot a V1/V=0.8377848691 arány adja. Tehát az Airy korongba az összes fényáram mintegy 84%-a kerül.
Lássuk most az első diffrakciós gyűrűt. Ehhez ugyanezt az integrált kell kiszámítani, csak az integrációs határok módosulnak. l1 marad ugyanaz mint fent,l2=7.015586670 a J1(x)=0 egyenlet második megoldása. e két érték adja az első diffrakciós gyűrű belső illetve külső peremét.
![[Maple Plot]](images/refreloszl13.gif)
Ennek értéke:
![[Maple Plot]](images/refreloszl14.gif)
R=1-re és q=1-re:
V2=2.848196726
Az első diffrakciós gyűrűbe jutó fényhányad:
V2/V=0.07214566585.
Az első diffrakciós gyűrűbe tehát a teljes fényáram kb 7.2%-a jut.
Megadjuk végre Vk általános képletét, k=3,4,5...-re:
![[Maple Plot]](images/refreloszl22.gif)
Végül íme itt az eredmény k=3-ra:
V3=1.094220902
Ezzel
V3/V=0.02771693923
A második gyűrűbe jutó fényhányad tehát kb 2.8 %.

![]()
![[Maple Plot]](images/res11.gif)

![[Maple Plot]](tav2.gif)
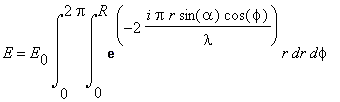
![[Maple Plot]](images/specmat1.gif)
![]()
![[Maple Plot]](images/specmat3.gif)
![[Maple Plot]](images/specmat4.gif)
![]()
![[Maple Plot]](images/specmat6.gif)
![[Maple Plot]](images/specmat7.gif)
![[Maple Plot]](images/res15.gif)
![[Maple Plot]](images/res16.gif)
![]()
![]()
![[Maple Plot]](images/res19.gif)
![[Maple Plot]](images/res20.gif)
![[Maple Plot]](images/res21.gif)
![[Maple Plot]](images/res22.jpg)
![[Maple Plot]](images/res23.gif)
![[Maple Plot]](images/res20.gif)
![[Maple Plot]](images/refreloszl4.gif)
![[Maple Plot]](images/refreloszl5.gif)
![[Maple Plot]](images/refreloszl6.gif)
![[Maple Plot]](images/refreloszl7.gif)
![[Maple Plot]](images/refreloszl8.gif)
![[Maple Plot]](images/refreloszl13.gif)
![[Maple Plot]](images/refreloszl14.gif)
![]()