2.Fényelhajlás (diffrakció) központi kitakarásos rendszerekben (Newtonok, katadioptrikus rendszerek)
|
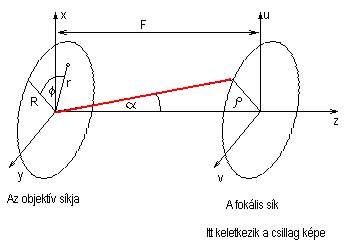
Itt is a probléma hengeres szimetriát mutat, így tehát illene az r,f, z
hengerkoordinátákat bevezetni.
Az útkülönbség:
r cos f sin a
A fáziskülönbség :
![[Maple Plot]](images/res10.gif)
Itt egy felületi integrált kell kiszámítani, mégbedig az xOy síkbeli R sugarú körlemezen lévő dS felületelemeken másodlagos hullámforrásokat helyezünk el, a Huyghens-Fresnel elvnek megfelelően.
Az innen kiinduló hullámokat összegezzük az alábbi kettős integrállal:
![[Maple Plot]](images/res11.gif)
|
Csakhogy itt az S felület, amin az integrálás végzendő, nem körlemez; ki kell vonnunk ebből a segédtükör felületét, hiszen innen nem érkeznek hullámok a kitakarás miatt. Jelöljük a segéftükör sugarát r0-lal.
Az integrál tehát:
![[Maple Plot]](images/nd1.gif)
Itt már integráltunk a f szög szerint, maradt az integrálás r szerint.
Ezt a lencsés távcsöveknél vázolt eljárással elvégezve a következő képlethez jutunk:
![[Maple Plot]](images/nd3.gif)
Itt is alkalmazható a kis a szögekre a sin a= tg a közekítés, így:
![[Maple Plot]](images/res17.gif)
és
![[Maple Plot]](images/nd4.gif)
Alkalmazzuk most a
![[Maple Plot]](images/nd5.gif)
jelölést! Ezzel
![[Maple Plot]](images/nd6.gif)
A fény intenzitáseloszlást E*Ekonjugált adja meg, de mivel az E valós,
E=Ekonjugált és így itt ez E2-ként számítható ki:
![[Maple Plot]](images/nd7.gif)
Itt tehát a r az Airy korong közepétől
mért távolság a fokális síkban, R a főtükör sugara, r0 a segédtükör
körvetületének a sugara. A 4p2E02-et
I0-val jelöljük,
![[Maple Plot]](images/nd8.gif)
Ellenőrzésképpen ha integrálunk a teljes fokális síkban, vissza kell kapjunk egy olyanmennyiséget, amely a kukkerunk fénygyűjtő területével arányos. Az integrál:
![[Maple Plot]](images/nd12.gif)
Integrálás után a következőt kapjuk:
![[Maple Plot]](images/nd14.gif)
Valóban, itt a p(R2-r02) = a főtükör területe - a segédtükör vetületének a területe.
Most megpróbálom szemléltetni a kitakarás hatását. Az egyszerűség kedvéért legyen R=1, q=1. Így p=r0/R, azaz a kitakarás ekkor egy 0 és 1 közötti szám lesz, továbbá p=r0 lesz az R=1 miatt.
Ezzel már viszonylag kényelmesen számolhatunk:
![[Maple Plot]](images/nd15.gif)
Lássuk, hogyan néz ez ki az I(r) grafikusan ábrázolva:
![[Maple Plot]](images/nd17.gif)
A fényeloszlás 3D diagramon ábrázolva:
![[Maple Plot]](images/ndj1.jpg)
A fokális síkra vetített csillagkép a fenti kép alapján számolva:
![[Maple Plot]](images/ndj2.jpg)
Látható, hogy a lencsés távcsövekhez képest az első diffrakciós gyűrű egy árnyalatnyival nagyobb.
A kitakarás hatása jobban látszik, ha a p értékét 0.5-re növeljük, majd az eredményeket ábrázoljuk.
Az 50 %-os kitakarás ugyan botrányosan nagy, de szemléltetésre megfelel.
3D diagram p=0.5-re:
![[Maple Plot]](images/ndj3.jpg)
A csillag képe:
![[Maple Plot]](images/ndj4.jpg)
Jól érzékelhető az első diffrakciós gyűrű erősödése, sőt, a második is!
Végül egy extrém eset: a p=0.9, azaz a 90 %-os kitakarás: sokan így próbálják
meg csökkenteni a nap megfigyelésekor a fényáramot. Az alábbi grafikonok
megmutatják, milyen jelentős a kontrasztcsökkenés, a fénycsökkenéssel párhuzamosan:
Tehát a 3D diagram p=0.9-re:
![[Maple Plot]](images/ndj5.jpg)
A csillag képe:
![[Maple Plot]](images/ndj6.jpg)
Háát...az Airy korongban alig marad fény, igen sok kerül át a diffrakciós
gyűrűbe.
A kontrasztcsökkenés katasztrofális.
Az amatőrcsillagászok kézikönyvében, a 61 oldalon található
egy táblázat arról, hogy a központi kitakarás milyen hatással van az
Airy korongba jutó fény hányadáról. Ellenőriztem a fenti képlettel a
táblázatot; az egyezés tökéletes.
Amennyiben a Newton távcsöveknek a tartólábait is figyelembe vesszük, akkor
a diffrakciós gyűrűk mellett megjelenik a négyágú tüske (négyágú tükörtartó esetén)
Nem tudom, mennyiségileg ez mit jelent pontosan. De azt mindannyian tapasztaltuk,
hogy jól látható a fényes csillagok körül. Sajnos csak akkor tudom analitikusan
kezelni a dolgot, ha a tükörtartó lábak vastagodnak a perem felé. Ekkor ugyanis a
hengerszimmetria megmarad. Ilyen tartólábat azonban csak a bolond szerelne a kukkerjába.
Marad a numerikus modellezés: ez azonban mellékhatásokkal jár...

![]()
![[Maple Plot]](images/res11.gif)

![[Maple Plot]](images/nd1.gif)
![[Maple Plot]](images/nd3.gif)
![]()
![[Maple Plot]](images/nd4.gif)
![]()
![[Maple Plot]](images/nd6.gif)
![[Maple Plot]](images/nd7.gif)
![[Maple Plot]](images/nd8.gif)
![[Maple Plot]](images/nd12.gif)
![[Maple Plot]](images/nd14.gif)
![[Maple Plot]](images/nd15.gif)
![[Maple Plot]](images/nd17.gif)
![[Maple Plot]](images/ndj1.jpg)
![[Maple Plot]](images/ndj2.jpg)
![[Maple Plot]](images/ndj3.jpg)
![[Maple Plot]](images/ndj4.jpg)
![[Maple Plot]](images/ndj5.jpg)
![[Maple Plot]](images/ndj6.jpg)