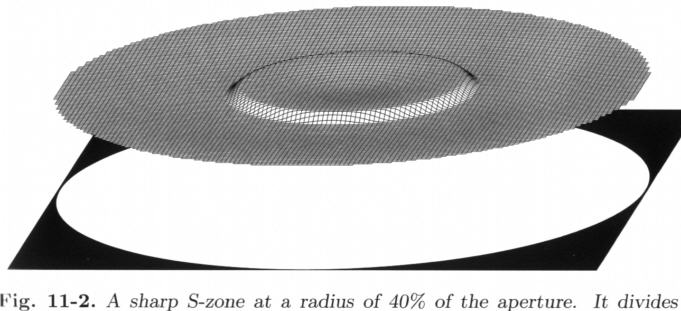
Autokollimációs távcsőteszt
(elméleti rész)

Felhasznált irodalom: Ingalls: Amateur Telescope Making Suiter: Star Testing Astronomical Telescopes

Bevezetés Az autokollimáció 2 lényeges eszközt tartalmaz: egy nagyméretű és igen jó minőségű síktükröt, melyet a tesztelendő távcső elé helyezünk, valamint egy szintén kiváló optikájú osztóprizmát, mellyel a műcsillag fényét az optikai tengelybe tükrözzük. Ennek az elrendezésnek köszönhető, hogy pontosan az optikai tengely mentén mérhetünk (ellentétben pl. a hagyományos Foucault teszttel), ráadásul kétszeres pontossággal, hisz a fény a távcső összes optikai elemén kétszer halad át, s így minden "torzítás" duplájára nő. Az elrendezés mellékterméke, hogy az osztóprizmába tükrözött műcsillag a távcső számára végtelen távol van, hisz az objektíven párhuzamos fénysugarak lépnek ki és be. Így például egy paraboloidtükörrel szerelt Newton távcső vizsgálata esetén (de minden más csillagászati távcsőnél is!) a tesztben látottak egy gömbtükör Foucault- Ronchi-, illetve csillagtesz-ábráinak felelnek meg, megkönnyítve a hibák felismerését. Ideális gömbtükör ugyanis mindig egyenes vonalú ábrát mutat: legyen az Ronchigram, vagy Foucault féle késélpróba. A csillagtesztet pedig változtatás nélkül használhatjuk. FONTOS! Ezen az oldalon mindig hullámfronton (és nem felületen) vett értékekről (hiba, eltérés, aberráció, PtV, RMS, stb...) beszélünk. Az ideális hullámfrontot mindig egy sík felülettel ábrázoljuk. Kapcsolódó irodalom: A titokzatos lambda. Ezen az oldalon bemutatjuk azokat a hibákat, melyeket az autokollimációs módszerrel kiszűrhetünk. 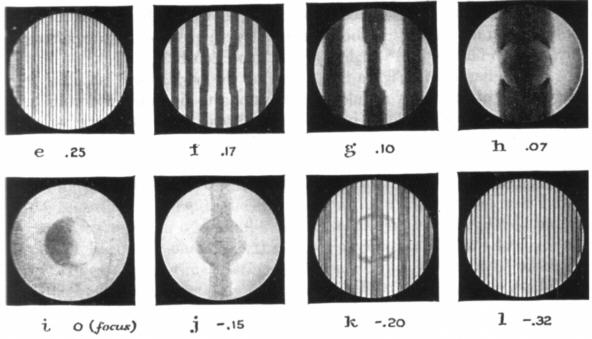Ezek rendre: Szférikus aberrációk (mindenekelőtt a W4 és W6 Zernike együtthatók) Zónahiba Peremkopás Polírozottság Asztigmatizmus (később) Három ponton megfeszített optika (később)

Szférikus aberráció A leggyakrabban előforduló hiba, mely a főtükör hibás mélyítéséből (Newton), a korrekciós lencsék helytelen görbületéből és elhelyezéséből (katadioptrikus távcsövek), vagy a légrés helytelen beállításából, a törésmutatók s a görbületek helytelen értékéből (refraktor) együttesen következik. Az alábbi ábra az alacsonyabb és magasabb rendű szférikus aberrációkra mutat be egy-egy példát. (idális hullámfronttól való eltérés 3D ábrája)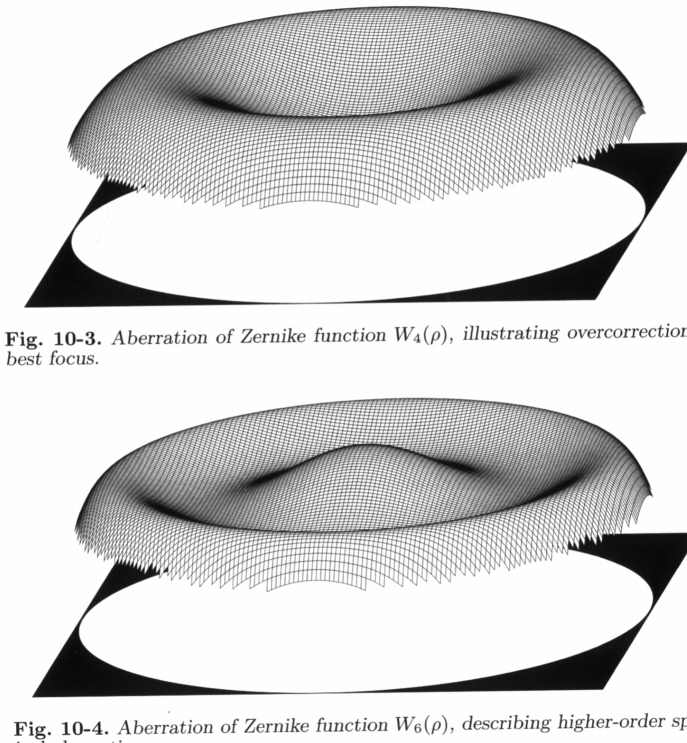 Műcsillagtesztünkben rendre a műcsillag extra és intrafokális képét hasonlítjuk össze. A felső 3 sorban egy refraktoron (kitakarás nélkül), alattuk egy 33%-os kitakarású tükrös távcsövön keresztül szemlélve. A nagyítást legalább akkorának válasszuk meg, mint a távcső milliméterben vett átmérője. Balról jobbra haladva közeledünk a fókuszhoz: 10 gyűrűt, majd 5-öt látunk, aztán az Airy korongot a diffrakciós gyűrűkkel, majd a fókuszon túlhaladva újra 5 és 10 gyűrűt. Teszteléshez mindig 5-10 gyűrűt állítsunk be, olyankor lehet a hibákat a legjobban felismerni. 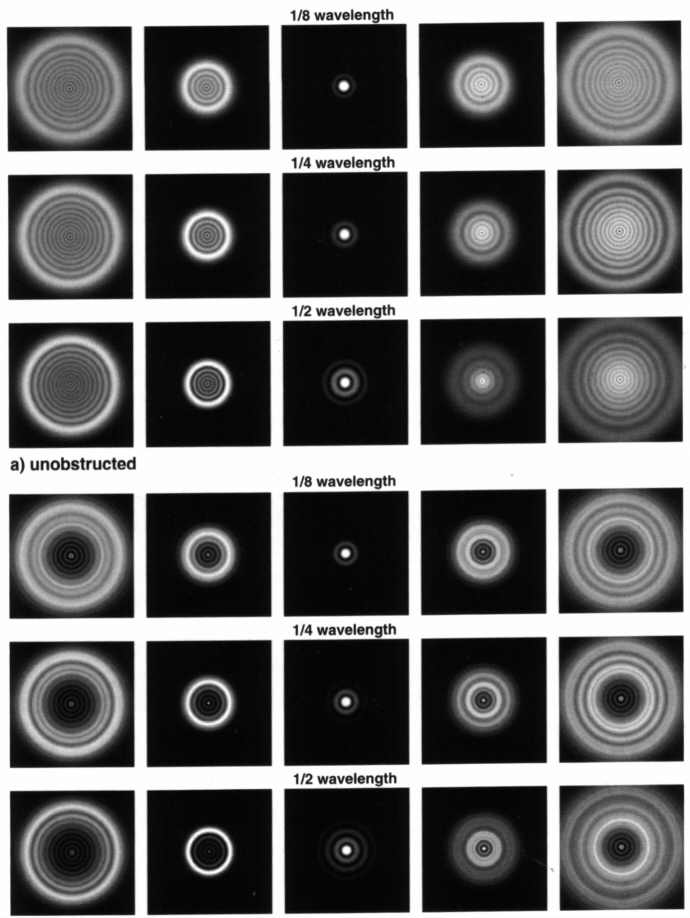Ideális esetben a műcsillag extra és intrafokális képe egymással teljesen megegyezik, a külső gyűrű határozott, de nem túl éles, és befelé haladva a gyűrűk intenzitása egyenletesen csökken. Szférikus aberráció hatására az extra és intrafokális képek egymástól egyre jobban eltérnek. A beszkennelt lapon feliratozott PtV "wavelenght" értékek ég alatti (azaz nem autokollimációs) csillagtesztre vonatkoznak: eszerint 1/8 kiváló, 1/4 diffrakcióhatárolt, 1/2 használhatatlan. Mi azonban (az autokollimációnak hála) kétszeres pontossággal mérünk, tehát az 1/2-del jelölt sor jelenti autokollimációban a diffrakcióhatároltság kritériumát (standard), míg az 1/4-del feliratozott hiba autokollimációban mindössze 1/8 hullámfronthibát (prémium) takar. A legfelső sorban írt 1/8 (autokollimációban 1/16) érték meghaladja síktükrünk felületi pontosságát. Hasonlóan értelmezhetőek a Ronchi rácson keresztül látottak, melyekről bővebben (végtelen távoli műcsillagot használva, de nem autokollimációban) itt olvashat. Végezetül álljon itt összehasonlításul 3 ideális felületű távcsőben látott diffrakciós és különböző mértékben defókuszált extrafokális kép, ha a kitakarás mértékét változtatjuk (fentről lefelé rendre 0%, 20%, 33%).

Zónahiba Másik gyakori hiba a zónahiba (S-Zone), melyből gyakran több is egymásra rakódik. A diffrakciós képben ez olyan összetett változásokat hoz létre, hogy szinte lehetetlen megállapítani, hogy hol és hány zónahiba rakódik egymásra. Ennek vizsgálatát Ronchi ráccsal, vagy Foucault féle késélteszttel végezzük. Ha csak egyetlen zónahiba van jelen, és más hiba (pl. szférikus aberráció) nem lép fel vele együtt, akkor az extra és intrafokális kép még elemzhető, ha nem is egyszerűen. A zónahiba ott van, ahol az extra- és intrafokális képben a gyűrűk intenzitása egymástól a legjobban különbözik. A balra lent az első és második képen feltűnő a belülről számított 3. és 4. gyűrű intenzitáskülönbsége (R=40%-nál), de ez a hiba kihat a kívülről számított 4. gyűrű környékére is. Ez utóbbi jelenség miatt nem lehet az egymásra rakódott zónahibákat a csillagteszttel egzakt módon megállapítani. Jobbra az ideális felületet látjuk, a felső sorban pedig a zónahiba fókuszált képre való hatást vizsgálhatjuk. Szerencsére a Foucault féle késél-teszt és a Ronchi rács lényegesen többet elárul erről a hibáról. Magyarázat helyett egyszerűen hasonlítsuk össze az alább bemutatott Foucault árnyképet a fotó alá rajzolt ábrákkal. A késél árnyéka egzaktul visszaadja az ideális hullámfronttól való eltérést! Csakúgy, mint a Ronchi rács, ha megfelelő a fókusztól való távolsága.

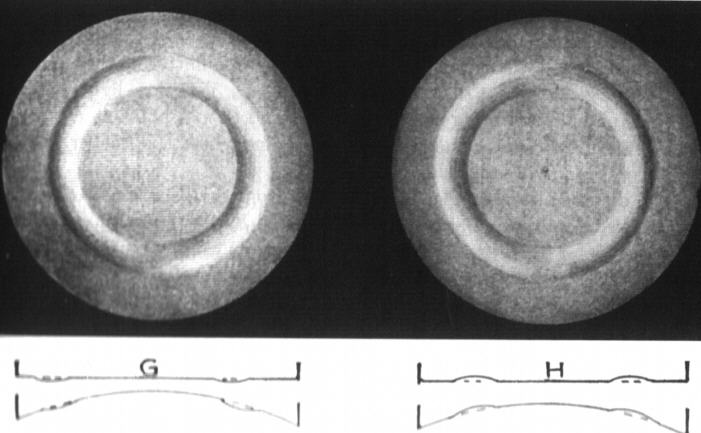
Peremkopás Szintén gyakori, de nem veszélyes hiba. A képalkotásra alig van hatással, szükség esetén blendézés is sokat segít. Ronchi ráccsal egyértelműen kimutatható.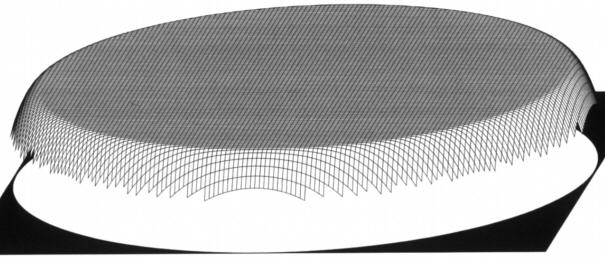 Se a fókuszált diffrakciós-, se az extra- és intrafokális képben nem hoz létre drasztikus változást ez a hiba, annak ellenére, hogy a peremkopás mértéke a bemutatott fotón 0.63 hullámhossznyi, azaz L/1.5 körüli. Ez is azt igazolja, hogy a PtV érték nem igazán jellemzi a felület jóságát. Nem mindegy, hogy hol helyezkedik el az a bizonyos "hegy-völgy" különbség. A kontraszt valamelyest csökken, mivel az Airy korongból az első gyűrűbe tolódik ki a fény. A bemutatott fotón fent a fókuszált kép (balra a peremkopott, jobbra az ideális), alattuk a peremkopott defókuszált képeit hasonlíthatjuk össze az ideálissal egy 25%-os kitakarású Newton távcsőbe nézve. 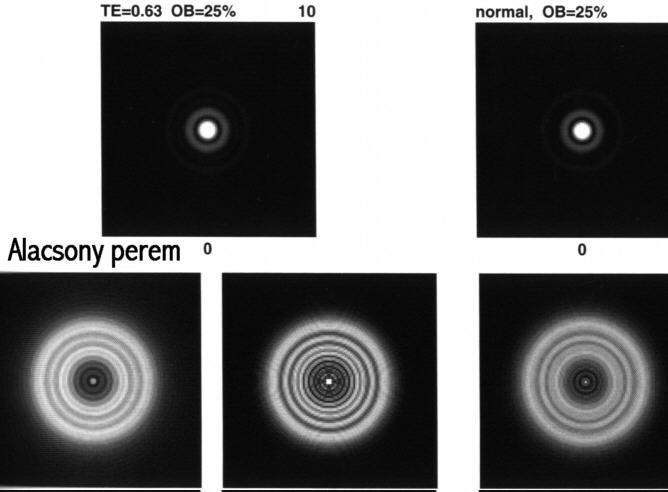A peremkopás Ronchi ábráit, valamint az eddig bemutatott hibákat bővebben itt tanulmányozhatja.

Polírozottság (RMS) Nagyon fontos tényező! Egy távcső akkor ad igazán jó képet, ha nem csak az ideális görbületeket találta el a gyártó, hanem a felület tisztességesen ki is van polírozva! A hanyag polírozás hasonló hatással van a diffrakciós képre, mint a nyugtalan légkör. Csak míg a légköri turbolencia időbeli változást hoz létre a diffrakciós képben (bővebben itt), addig a gyenge RMS érték által létrehozott kép állandó marad. Az alábbi képeken egy kiválóan, egy nagyon jól és egy átlagosan felpolíroztt (egyébként ideális felületű) Newton távcső extra és intrafokális fotóját mutatjuk be. Összehasonlításképpen: a diffrakcióhatároltság kritériuma a hullámfrontra vonatkoztatva RMS=1/14 lambda.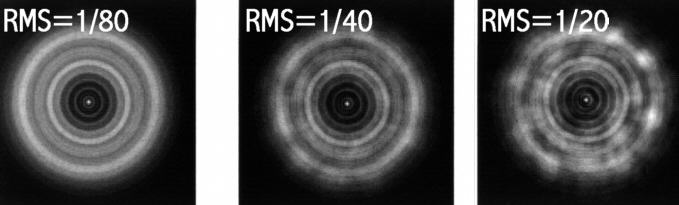

Asztigmatizmus (később)

Három ponton megfeszített optika (később)